Cho em hỏi về toán một tẹo

Em cảm ơn chị Vân nhiều lắm:x Chị giải thích dễ hiểu lắm mà :x Túm lại là Ham Sandwich Cut Theorem nói rằng luôn tồn tại một mặt (n-1) chia mặt n ra làm 2 tập con/vùng nhỏ bằng nhau. Và bài này thì n=2 nên hyperplane là 1 đường thẳng.

Bài này em đã nhờ được 2 người giải thích cho bằng 2 cách khác nhau. Một người dùng đến HSCT, người còn lại không dùng. Ặc, thế nên em mới bị 'lẫn'.

Người thứ nhất nói rằng bài toán của em là ví dụ kinh điển của "Ham Sandwich Cut Theorem" . Bài này tên là "Trộm chia vòng". Tức là có 2 tên trộm cướp được một chiếc vòng trên đó có chẵn các hạt Kim Cương và Rubi sắp xếp không theo một thứ tự nhất định nào cả. Số lần cắt vòng ít nhất là bao nhiêu để mỗi tên nhận được số Kim Cương và Rubi bằng nhau.
Đây là những trường hợp xảy ra:
1. Số Kim Cương và Rubi được sắp xếp xen kẽ nhau:
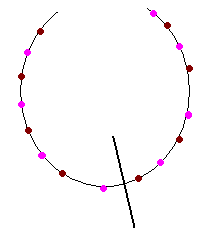
theive1.gif

2. Số Kim Cương và Rubi được xếp đều về 2 phía:
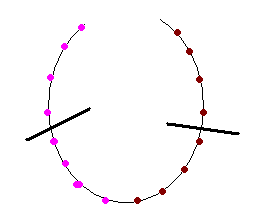
theive2.gif

3. Đặt chiếc vòng lên một đường parabol. Nếu một đường thẳng giao với parabol thì nó sẽ cắt parabol tại 2 điểm. Thế là ..Xong !
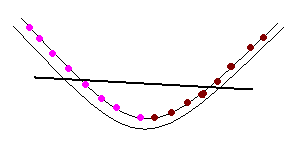
theive3.gif

Hị Hị, đọc đến đây em mới thắc mắc, nếu các hạt Rubi và Kim cương được xếp kiểu ngẫu hứng, không theo một thứ tự nào thì làm sao có luôn có thể chia đường parabol đó ra thành 2 phần chứa số Rubi và Kim cương bằng nhau. VÍ dụ như một dây sắp xếp ntn : 1 Rubi-3 Kim cương-7 Rubi-9 Kim cương.


Ặc, nhưng lại có một người thứ 2 giải thích cho em bài này mà không dùng đến HSCT. Em thấy cách giải thích này logic hơn.

Số viên Kim cương: 2m. Số viên Ngọc : 2n.
Lấy 1 con dao có 2 mặt A, B. Cắt theo đường kính, chia vòng làm 2 phần. Nửa A có X viên Kim Cương. Nửa B có 2m-X . Giả sử X=<2m-X. Nếu xoay dao (m+n) vị trí, mặt A lại có 2m-X, mặt B có X viên Kim Cương.
Khi xoay dao từ vị trí 1 đến (m+n), xảy ra một lần sao đi qua điểm sao cho
X=2m-X
<=>X=m=1/2 tổng số Kim Cương
Tổng Rb và Kc ở mặt A= mặt B=2(m+n)/2=(m+n)=> Nếu số Kc bị chia đôi thì số Rb ở mỗi nửa cũng bị chia đôi.
Í ẹ, túm lại là nếu áp dụng định lý HSCT thì chẳng cần chứng minh gì, chị Vân nhỉ? Em thắc mắc ở cái đấy. Vì nếu áp dụng kô thôi thì bài toán này..ngu quá, như kiểu một ví dụ của HSCT ý. Em muốn hiểu phần CM, nhưng đọc chứng minh của HSCT mà sao trăng bay ngập trờib-( Thế bài này có được xếp vào dạng tập hợp không chị Vân:?:Em thấy nó giống.. toán vui :mad:)
 
Chỉnh sửa lần cuối:
2 người gì hả Phương, cả 2 cách đấy tớ google ra đều có mà, giống hệt. Không cần phải nhân hóa thế đâu. :D Mà cách 2 của ấy cũng từ Ham Sandwich Cut Theorem mà ra, chỉ là cách giải thích cho trường hợp cụ thể là có 2 tập con.
 
Nguyen Khac Son đã viết:
2 người gì hả Phương, cả 2 cách đấy tớ google ra đều có mà, giống hệt. Không cần phải nhân hóa thế đâu. :D Mà cách 2 của ấy cũng từ Ham Sandwich Cut Theorem mà ra, chỉ là cách giải thích cho trường hợp cụ thể là có 2 tập con.
Nhấn để mở rộng...
vô duyên [-( Cách 2 một người quen tớ giải cho mà :p Sơn vô duyên :p nghỉ chơi với ấy à nha [-(

Cách 2 đâu có dùng HSCT nhẩy? Mà cũng tại HSCT chứng minh tớ đọc toét cả mắt chả hiểu gì b-( Ấy là tớ muốn nhờ mấy bác Toán giải thích hộ cho cái đống lùng bùng ấy 0:)

Mắng tiếp : Sơn vô duyên hihi :p Tớ mà được thêm 7 điểm chất lượng nữa tớ trừ điểm ấy luôn :p Mà đi ngủ đêeeeeeee...biết mấy giờ rồi kô?
 
Chỉnh sửa lần cuối:
Uha cách 2 là CM cụ thể của t/h n=2 áp dụng cho bài của em Phương :) Chứ CM cho t/h n=2 nói chung thì diễn giải ra nó cũng hơi khang khác 1 tí tẹo
Em Sơn bên ngoài có dễ thương như avatar ko nhỉ :x
 
Ah quên thế ko em/anh/chị nào chấm điểm cho bài giải Ham Sandwich Cut Theorem của mình à :((
Đùa tí, tại em Phương nhắc đến điểm chác chị mới để ý :p Ko hiểu mấy ng ở CLB Học tập có đc điểm bao giờ ko. Hay là điểm chỉ đc chấm cho bài văn thơ hay bài viết hay chứ ko đc chấm cho việc ngồi giải toán lý hóa :-/
 
Nguyễn Hà Phương đã viết:
Thế bài này có được xếp vào dạng tập hợp không chị Vân:?:Em thấy nó giống.. toán vui :mad:)
Nhấn để mở rộng...
Borsuk Ulam Theorem chị chỉ biết ở mảng Topology/ Multidimensional analysis
 
Chỉnh sửa lần cuối:
www.mathlinks.ro/Forum/
Day la mot forum rat quen thuoc voi dan Toan. Mot dieu kha hay la co rat nhieu nguoi Viet Nam tham gia forum nay (Trong do co ca nhung cao thu IMO - 2004 cua Viet Nam nhu Le Hung Viet Bao, Nguyen Minh Truong)
 
Bây giờ thay đổi không khí bằng các bài toán thi Đại học nào:
1. CMR: sin(pi.x/2)>2.x^2/(1+x^2) với mọi 0<x<1
2. CMR (sinx/x)^2p +(tgx/x)^p>2 với mọi 0<x<pi/2 , p>0
Để cho dễ ta xét p = 1 trước đã.
3.CMR pi<sin(pi*x)/[x(1-x)]<4 với mọi 0<x<1/2
4.CMR (sinx)^sinx < (cosx)^cosx với mọi 0<x<pi/4
 
Thầy Thái:Có 21 hs nam va 21 hs nữ.Biết rằng cứ 1hs nam và 1 hs nữ thì có ít nhất một bài toán giải chung và không có hs nào trong 42 hs giải được quá 6 bài toán.CMR tồn tại 3hs nam và 3hs nữ cùng giải được 1 bài toán.
 
Đây là đề IMO 2001 mà :eek:. Em này lạ thật, đề IMO mà cũng không biết lời giải à?? b-) .
 
Thôi, dù sao cũng trả lời chú em luôn!! Chuyển bài toán về dạng ma trận cái đã ( vụ này dễ thôi, nhưng vấn đề là nghĩ ra nó :( )!! Lời giải tiếp theo như sau: (chịu khó đọc tiếng Anh nhé ;) )

Problem:

Integers are placed in each of the 441 cells of a 21 x 21 array. Each row and each column has at most 6 different integers in it. Prove that some integer is in at least 3 rows and at least 3 columns.



Solution :


Notice first that the result is not true for a 20 x 20 array. Make 20 rectangles each 2 x 10, labelled 1, 2, ... , 20. Divide the 20 x 20 array into four quadrants (each 10 x 10). In each of the top left and bottom right quadrants, place 5 rectangles horizontally. In each of the other two quadrants, place 5 rectangles vertically. Now each row intersects 5 vertical rectangles and 1 horizontal. In other words, it contains just 6 different numbers. Similarly each column. But any given number is in either 10 rows and 2 columns or vice versa, so no number is in 3 rows and 3 columns. [None of this is necessary for the solution, but it helps to show what is going on.]

Returning to the 21 x 21 array, assume that an arrangement is possible with no integer in at least 3 rows and at least 3 columns. Color a cell white if its integer appears in 3 or more rows and black if its integer appears in only 1 or 2 rows. We count the white and black squares.

Each row has 21 cells and at most 6 different integers. 6 x 2 < 21, so every row includes an integer which appears 3 or more times and hence in at most 2 rows. Thus at most 5 different integers in the row appear in 3 or more rows. Each such integer can appear at most 2 times in the row, so there are at most 5 x 2 = 10 white cells in the row. This is true for every row, so there are at most 210 white cells in total.

Similarly, any given column has at most 6 different integers and hence at least one appears 3 or more times. So at most 5 different integers appear in 2 rows or less. Each such integer can occupy at most 2 cells in the column, so there are at most 5 x 2 = 10 black cells in the column. This is true for every column, so there are at most 210 black cells in total.

This gives a contradiction since 210 + 210 < 441.
 
Hóa ra đây là đề thi IMO 2001 à?Bây giờ em mới biết...Nhưng thày Thái giải khác...Thày đánh giá số cầu là >441 cơ.Cách giải này thì đúng rồi.Cám ơn anh nhiều!
 
Nguyễn Hoàng Mai đã viết:
em hỏi chút (sqt2) ^ (sqt2) là rational or irrational ạ?
Nhấn để mở rộng...
sqrt chứ nhỉ (square root)
irrational (đoán :) )
 
Chỉnh sửa lần cuối:
em cũng ko rõ nữa em chưa học đến transcendental nên ko biết làm thế nào để xác định 1 số có phải là transcendental hay ko...
hình như chưa có ai cm là sqrt2 ^ sqrt2 là rational or irrational thì phải
 
Bạn phải đăng nhập hoặc đăng ký để phản hồi tại đây.
Back
Bên trên