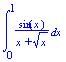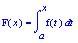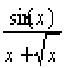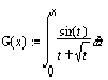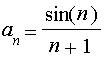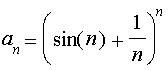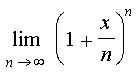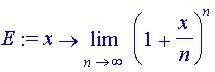Chủ đề Hàm số
a)
Khái niệm hàm số
Hàm số là một chủ đề không dễ dạy trong chương trình phổ thông, và có không ít thầy cô muốn bỏ qua chủ đề này. Cái khó là ở chỗ: chủ đề này luôn được xem là then chốt, mà lại chẳng có gì để dạy. Ngoài câu định nghĩa khá trừu tượng “
hàm số” là một phép
cho tương ứng mỗi số x (trong miền xác định)
với một số y (trong miền giá trị) …” người thầy chỉ còn biết viện ra vài biểu thức đại số quen biết để minh họa (thường là các đa thức, phân thức với biến x), và kết quả là phần lớn học sinh luôn hiểu nhầm hàm số là một biểu thức đại số. Muốn cho học sinh có được cái nhìn toàn diện hơn về hàm số thì phải có được các minh họa có tính thuyết phục hơn,
phải cho học sinh thấy được phép ứng là một khái niệm tổng quát hơn là việc tính giá trị của biểu thức đại số thông thường. Máy tính là một công cụ hỗ trợ rất tốt cho thầy trong tình huống này. Sau đây là ví dụ về một hàm số “chưa quen thuộc” nhưng thể hiện một cách rất rõ nét bản chất “phép ứng” của hàm số (dĩ nhiên các thầy có thể tìm nhiều hàm đơn giản hơn cho học sinh dễ hiểu, ở đây chỉ trình bày một thiứ dụ có tính điển hình và phục vụ cho việc đi xa hơn sau này).
Trong phần
giới hạn dãy số chúng ta đã biết rằng với mỗi số x thì
giới hạn của dãy số sau đây là tồn tại
Như vậy, ta có thể thiết lập được một phép ứng: cho mỗi số x tương ứng với giá trị của giới hạn dãy số nêu trên. Khi ấy, theo định nghĩa, ta có được một hàm số và có thể ký hiệu nó là E(x), tức là:
Cho đến nay, những hàm số kiểu này còn ít được xem xét là vì việc tính giá trị của nó (bằng thủ công) thường rất khó khăn, ngoại trừ tại một số điểm rất đặc biệt. Máy tính chính là phương tiện hỗ trợ đắc lực cho ta khắc phục vấn đề này. Máy dễ dàng tính cho ta giá trị của hàm tại bất kỳ điểm nào. Trước hết ta dạy cho máy biết định nghĩa của hàm số bằng câu lệnh theo đúng ngôn ngữ toán học đời thường:
[>
E:=x->limit((1+x/n)^n,n=infinity);
Sau khi cho thực hiện lệnh (cũng tức là khai báo xong hàm số), ta có thể tính giá trị của hàm số tại bất kỳ điểm nào. Chỉ xin lưu ý rằng giá trị của hàm thường là những
số vô tỷ "lạ hoắc" mà ta chưa từng biết đến (và do đó chưa có ký hiệu biểu diễn), cho nên muốn nhận biết nó thì cần dung lệnh xem xấp xỉ thập phân (với độ chính xác do ta tùy chọn), như ta vẫn thường làm với các số vô tỷ quen biết khác. Thí dụ, muốn biết giá trị của hàm tại một số điểm như
x=1.25,
x=2.3,
x=-0.7 … (với độ chính xác tới 50 chữ số thập phân chẳng hạn) ta sử dụng các lệnh:
[> evalf(E(1.25),20);
3.4903429574618413761
[> evalf(E(2.3),20);
9.9741824548147207400
[> evalf(E(-0.7),20);
0.49658530379140951470
Cứ như vậy, ta có thể tính giá trị của hàm tại bất kỳ điểm nào. Và như vậy, hàm số E(x) đã được xác định theo đúng bài bản định nghĩa.
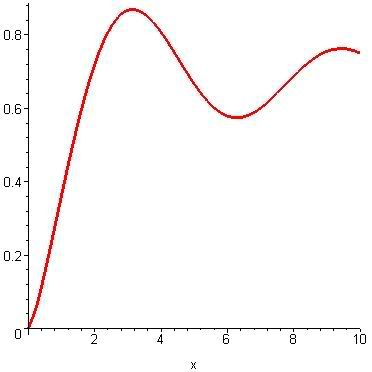
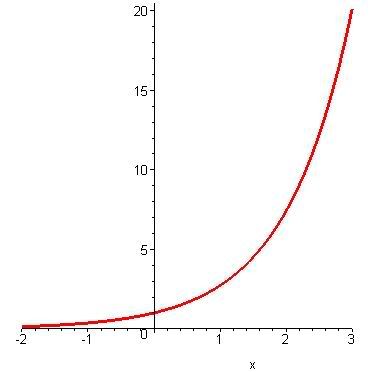
Một điều cần lưu ý là máy tính xử lý các hàm số không quen thuộc kiểu này cũng giống hệt như các hàm số bình thường. Nghĩa là ta có thể tính giới hạn, xét tính liên tục, lấy đạo hàm, vẽ đồ thị … của nó một cách dễ dàng. Ví dụ, ta cho máy vẽ đồ thị của hàm trên đoạn [-2,3] bằng lệnh
[>
plot(E(x),x=-2..3);
Thực ra, những hàm số
phải tính nhờ máy (như hàm kiểu này) không phải là ít gặp. Các hàm
lượng giác là những ví dụ khá điển hình, và quen thuộc hơn nữa hơn là những hàm có chứa căn thức.
b)
Hàm số mũ
Những người tìm hiểu sâu về toán đều biết rằng
hàm số mũ là một chủ đề khó, khó ngay từ khâu định nghĩa
lũy thừa bậc vô tỷ của một số. Trong các sách giáo khoa phổ thông (lớp 11-12) hiện nay việc định nghĩa
hàm số mũ chỉ mang tính phiến diện, cốt sao cho học sinh thừa nhận rằng lũy
thừa bậc vô tỷ cũng giống như
lũy thừa bậc hữu tỉ. Các sách giáo khoa đại học ở ta thì lại coi hàm số mũ là một khái niệm đã biết từ phổ thông nên cũng không cho một định nghĩa chính xác. Vấn đề đặt ra: Liệu có thể định nghĩa một cách nghiêm túc về mặt toán học hàm số mũ trong chương trình phổ thông hay không ?
Câu trả lời là có thể !
Về mặt lý thuyết thuần túy, điều này thực hiện được nhưng không phải là dễ dàng, nhất là với các học sinh dưới trung bình.
Bằng sự hỗ trợ của phần mềm và máy tính, ta có thể làm cho việc này trở nên dễ dàng hơn đối với mọi đối tượng. Hãy nhớ lại hàm số E(x) mà ta định nghĩa trong phần trên. Máy tính đã giúp ta tính mọi giá trị của nó một cách dễ dàng. Tuy nhiên, không chỉ có vậy, máy còn có thể kiếm chứng một số tính chất (định tính) rất thú vị của nó, mà việc chứng minh trực tiếp (bằng thủ công) là không dễ chút nào.
Trước hết, chúng ta hãy kiểm định một sô tính chất sau đây:
Tính chất 1:
(i)....E(0) =1
(ii)...O < E(x) với mọi x
(iii)...E(x+y)=E(x)E(y)
(iv)...E(-x)=1/E(x)
Kiểm định. Các tính chất (i) và (ii) kiểm tra dễ dàng bằng định nghĩa mà không cần tới máy tính (xin các bạn hãy tự kiểm đinh).
Tính chất (iii) và (iv) là không dễ chứng minh, cho nên ta sẽ cần tới sự trợ giúp của máy tính. Muốn vậy, ta sẽ hỏi máy rằng (với định nghĩa hàm E như trên) phải chăng các tính chất này là đúng ? Câu lệnh cũng được viết hoàn toàn theo ngôn ngữ đời thường (bằng tiếng Anh):
[>
is(E(x+y)=E(x)*E(y));
true
[>
is(E(-x)=1/E(x));
true
Sau khi cho thực hiện, ta thấy máy cho trả lời là đúng (true). Điều này cũng có thể chứng minh được một cách trực tiếp, nhưng phải là một học sinh giỏi (thậm chí phải rất giỏi) mới có thể tự chứng minh được điều này (xin các bạn hãy tự kiểm tra).
Ta đã biết cách định nghĩa khái niệm lũy thừa bậc hữu tỉ của một số bất kỳ (thông qua phép nâng lên lũy thừa bậc nguyên dương và phép khai căn) và biết các tính chất đặc thù của nó, thí dụ như
a[sup]p+q[/sup]=a[sup]p[/sup]a[sup]q[/sup] và a[sup]-p[/sup]= 1/a[sup]p[/sup] với mọi số hữu tỉ p và q
Rõ ràng, do (iii) và (iv), hàm số E(x) cũng có những tính chất đặc thù giống như là lũy thừa của một số. Tính chất sau đây còn cho thấy rõ hơn điều này.
Tính chất 2
Ký hiệu E(1) là e. Khi ấy ta có
E(x) = e[sup]x[/sup], nếu x là số hữu tỷ
(Tính chất này có thể chứng minh trực tiếp nhờ phép qua giới hạn dưới dấu lũy thừa và căn thức mà không cần tới sự trợ giúp của máy tính, xin các bạn hãy tự kiểm định điều này).
Tính chất trên mach bảo cho ta cách khai triển khái niệm lũy thừa của số e từ miền các số hữu tỉ ra toàn bộ trục số, bằng cách đặt giá trị của nó tại các điểm còn lại (vô tỷ) là giá trị của hàm E(x). Tức là
e[sup]x[/sup] = E(x) với mọi số thực x
Tính chất 1 cho thấy rằng lũy thừa e[sup]x[/sup] trên toàn bộ trục số cũng có những tính chất đặc thù giống như là trên tập các sỗ hữu tỷ, cụ thể là
e[sup]x+y[/sup]=e[sup]x[/sup]e[sup]y[/sup] và e[sup]-x[/sup]=1/e[sup]x[/sup]
Như vậy ta đã có được định nghĩa của hàm số mũ (cơ số e) trên toàn bộ trục số, theo đúng bài bản và logic. Không khó khăn lắm, ta có thể chứng minh được tính đồng biến của hàm e[sup]x[/sup] và do đó ta có thể định nghĩa được hàm ngược của nó, ký hiệu là ln(x) và đặt tên là hàm logarit tự nhiên.
Dễ dàng thấy rằng hàm số mũ với cơ số a bất kỳ (cũng như lũy thừa bậc vô tỷ của một số a bất kỳ) có thể được định nghĩa (biểu diễn) thông qua hàm số e[sup]x[/sup] và hàm logarit tự nhiên, như đã biết trong các sách giáo khoa.